반응형
중1 수학. 일차방정식 활용 소금물 문제 풀이
문제.
$10\%$의 소금물 $300g$이 있다. 여기에 몇 $g$의 소금을 더 넣으면 $20\%$의 소금물이 되는지 구하시오.
필요개념
$소금의 양=\frac{농도}{100}\times 소금물의 양$
풀이.
자세한 풀이과정은 아래 사진을 참고하셔도 됩니다.
소금물 문제는 표를 이용하여 문제를 해결하는 것이 좋다.
그리고 소금의 양을 이용하여 식을 세우면 된다.
먼저 농도 $10\$$소금물에 대한 소금의 양은 $\frac{10}{100}\times 300$이다.
더불어 소금을 더 넣었기 때문에 소금의 농도는 $100\%$이고 더 넣은 소금의 양$x~g$이라 하자.
그 두 개를 섞어서 농도가 $20\%$소금물이 되었을 때, $20\%$에 대한 소금의 양은
$\frac{20}{100}\times\left(300+x\right)$이다.
이렇게 소금의 양을 각각 구한 후에, 문제를 보면 섞었기 때문에 소금의 양을 더한 식을 세워주면 된다.
자 그럼 일차방정식을 세우면 아래와 같다.
$\frac{10}{100}\times 300+x=\frac{20}{100}\left(300+x\right)$
양변에 $100$을 곱하여 분수를 없애자.
$3000+100x=6000+20x$
이제 식을 정리하여 $x$를 구하면 된다.
$80x=3000$
$x=\frac{75}{2}$
따라서 더 넣은 소금의 양은 $\frac{75}{2} g$이다.
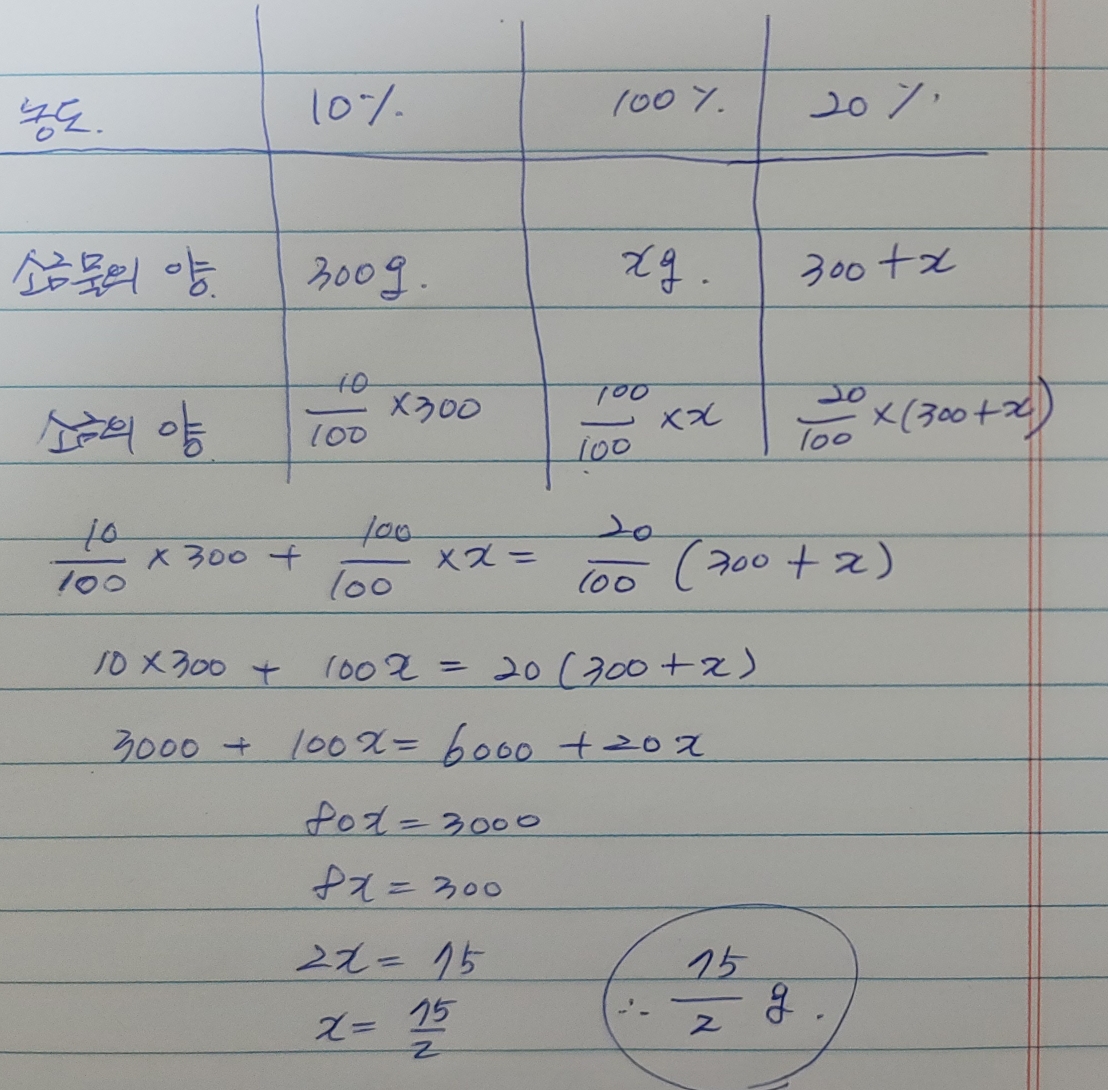
반응형
'중고등 수학' 카테고리의 다른 글
| 중2 수학. 대표를 뽑는 확률, 경우의 수 문제 풀이. (0) | 2023.10.13 |
|---|---|
| 중1 수학. 일차방정식의 활용- 학생수 문제 (0) | 2023.10.12 |
| 중2 수학. 식의 대입, 어떤 문자에 관하여 정리하기 (0) | 2023.10.10 |
| 중1 수학. 직각, 둔각, 예각 문제 풀이 (53) | 2023.10.09 |
| 중2 수학. 식의 계산 문제 풀이 (50) | 2023.10.08 |