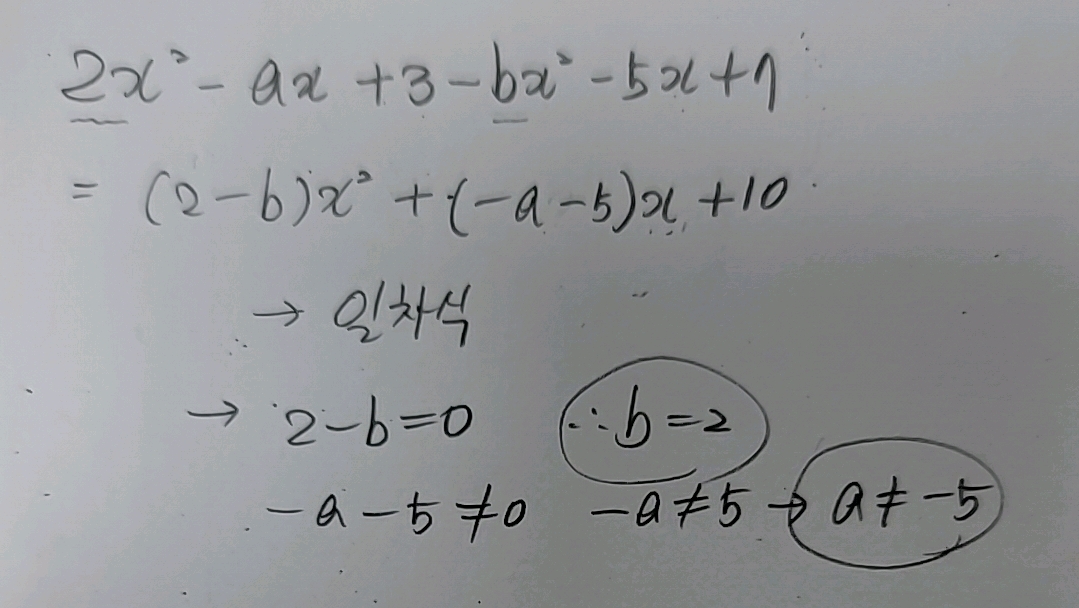교육

중1 수학. 일차식이 되기 위한 조건 문제. 다항식 $2x^{2}-ax+3-bx^{2}-5x+7$이 $x$에 대한 일차식이 되기 위한 상수 $a,~b$의 조건은? 개념 일차식이란 무엇일까? $ax+b$, 단 $a\neq0$일 때 일차식이다. 즉 $2x-4,~9x+1$과 같은 모양이 일차식이다. $2x^{2}-4x+2$은 일차식이 아닌 이차식이 된다. 풀이. 문제를 다시 한번 살펴보자. 다항식 $2x^{2}-ax+3-bx^{2}-5x+7$이 $x$에 대한 일차식이 되기 위한 상수 $a,~b$의 조건은? 이 식을 일차식의 모양으로 바꾸기 위해 우선 동류항끼리 계산을 하자. $2x^{2}-ax+3-bx^{2}-5x+7$ $=\left(2-b\right)x^{2}+\left(-a-5\right)x+10$ 이 식..

일차식의 계산. 괄호 풀기문제.다음 식을 계산하여라. 1. $\left(-5x+2\right)-\left(2x+7\right)$ 2. $\left(2x+5\right)-\left(-4x-3\right)$ 3. $\left(120x+7\right)-\left(6x-5\right)$ 필요한 개념1. 분배법칙 $a\left(b+c\right)=ab+ac$ 2. 음수와 음수의 곱셈 $\left(-2\right)\times \left(-3x\right)=\left(-2\right)\times\left(-3\right)x=6x$ 3. 동류향끼리는 계산할 수 있다. $x+y+2x+4y=3x+5y$ 풀이.1. $\left(-5x+2\right)-\left(2x+7\right)$ $=-5x+2-2x-7$ $=-7x-5$..

중1 수학. 일차방정식 일차방정식 일차방정식이란 우변의 모든 항을 좌변으로 이항 하여 정리했을 때 ($x$에 대한 일차식)=$0$의 꼴이 나타나면 된다. 좀 더 수학적으로 나타내면 $ax+b=0$, 단 $a\neq0$이다. 이렇게 개념적으로만 살펴보면 문제를 해결하는데 어려움이 있을 것이다. 실제로 예를 들어보자. $2x-1=3+x$에서 모든 항을 좌변으로 이항해 보자. $2x-x-1-3=0$이다. 이제 항을 정리하여 계산해 보자. $x-4=0$이다. 이 식은 $ax+b=0$의 모양인데, 이때 $a=1,~b=-4$인 것이다. 따라서 $2x-1=3+x$은 일차방정식이다. 다시 한번 또 살펴보자. $6x-8$이라는 식을 살펴보자. 이 식은 중요한 것이 $=$가 없다. 따라서 방정식이 아니다. 하지만 $6x-..

대입, 식의 값, 다항식과 일차식 개념. 대입과 식의 값 1. 대입 대입이란 문자를 사용한 식에서 문자를 수로 바꾸어 넣는 것이다. 예를 들면 $x=2,~y=3$일 때 $2x-y=2\times 2 -3$이렇게 바꾸는 것이 대입이다. 2. 식의 값 식의 값이란 문자를 사용한 식에서 문자에 수를 대입하여 계산한 결과이다. 예를 들면 방금 대입의 예에서 계산까지 하면 식의 값이 나오는 것이다. 즉, $x=2,~y=3$일 때 $2x-y=2\times 2 -3=1$이다. 3. 참고 (1) 문자에 어떤 수를 대입할 때에는 생략된 곱셈 기호인 $\times$를 다시 써주는 것이 좋다. (2) 문자에 음수를 대입할 때에는 반드시 괄호를 사용하여 나타내자. (3) 분모에 분수를 대입할 떄에는 생략된 나눗셈 기호인 $\d..

일차방정식 일차방정식이란 방정식에서 우변의 모든 항을 좌변으로 이항하여 정리하였을 때, $$\left(x에 대한 일차식\right)=0$$ 의 꼴이 되는 방정식이다. 몇가지 예를 들어 일차방정식인지 아닌지를 살펴보자. $$2x+1=x-5$$ $$2x+1-x+5=0$$ $$x+6=0$$ 첫번째 줄의 식에서 두 번째 줄의 식이 된 이유는 모든 항을 좌변으로 이항하였기 때문이다. 두 번째 줄의 식에서 세번째 줄의 식으로 된 이유는 동류항을 계산하여 좌변을 정리하였기 때문이다. 세번째 줄의 식에서는 $\left(일차식\right)=0$꼴이 되므로 이 식은 일차방정식이 된다. $$4x^{2}+1=4x^{2}-x+1$$ $$4^{2}+1-4x^{2}+x-1=0$$ $$1+x-1=0$$ $$x=0$$ 마지막 줄의 식..

분수 꼴인 일차식의 덧셈과 뺄셈 분수 형태의 일차식의 덧셈과 뺄셈은 첫째, 최소공배수로 통분을 한다. 둘째, 분배법칙을 이용하여 괄호를 푼다. 셋째 동류항끼리 계산을 한다. 자 이게 개념이다. 아래의 예를 통해 이해해 보자. $$\frac{x+3}{2}+\frac{x-2}{3}$$ $$=\frac{3\left(x+3\right)+2\left(x-2\right)}{6}$$ $$=\frac{3x+9+2x-4}{6}$$ $$=\frac{5}{6}x+\frac{5}{6}$$ 첫 줄의 식에서 두 번째 식으로 넘어갈때는 분모의 2와 3의 최소공배수인 6으로 통분하였다. 두번째 줄에서 세 번째 식으로 진행될 때에는 분배법칙을 이용하여 괄호를 풀었다. 세번째 줄에서 네 번째 줄로 진행될 때에는 동류항끼리 계산하였다. ..

차수와 일차식 차수란 어떤 항에서 문자가 곱해진 개수이다. 다항식의 차수란 다항식에서 차수가 가장 큰 항의 차수를 말한다. 더불어 일차식이란 차수가 1인 다항식이다. 이렇게 장황하게 글만 표현하면 도저히 알 수 없기에 만은 예를 들어 보도록 하겠다. $2x$는 $x$가 한번 곱해졌기 때문에 $x$에 대한 일차식이다. $2a^{2}-1$은 $a$가 제곱이다. 즉 $a$가 두 번 곱해졌기 때문에 $a$에 대한 이차식이다. 그럼 $7$은 몇차식일까? $7$은 $0\times x +7$이므로, 문자 $x$가 $0$번 곱해졌다. 따라서 0차식이 된다. $x^{2}-3x+1$은 $x$가 두번 곱해졌으므로, 이차식이 된다. $x^{2}= x \times x$라는 뜻이다. 또한 $-3x$에서는 $x$가 한번 곱해져 있..