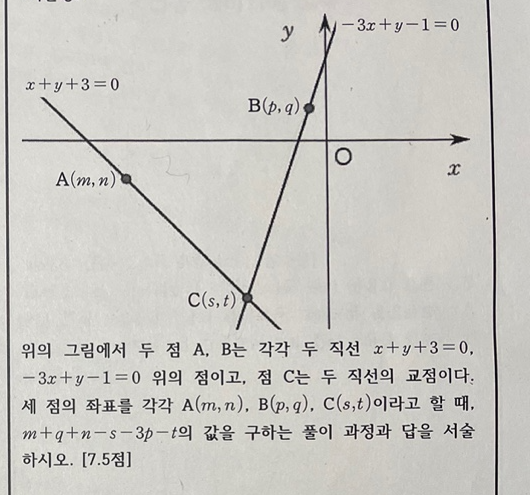
일단 이 문제는 크게 어렵지 않은 문제이다.
그러나 학생들은 많이 틀렸을 것이다.
그 이유는 무엇일까?
문제마지막줄에 구하라고 하는 $m+q+n-s-3p-t$를 구하라고 되어있다.
이것을 보자마자 대부분의 학생은 $m, q, n, s, p, t$를 구하려고 덤벼들 것이다.
택도 없는 소리!
이런 것을 구하기보다 문제의 본질을 살펴보는 것이 중요하다.
이래서 기본 개념이 중요하다는 것이다.
자 잔소리는 그만하고 풀이를 해보겠다.
이 문제에서 원하는 것은 직선 위의 점이 있다면 그 점을 다시 직선에 대입해도 성립한다는 것이다.
즉 $x+y+3=0$이라는 직선은 $A \left(m,n\right)$과 $C \left(s, t \right)$를 지난다.
즉 $x+y+3=0$이라는 직선에 $A$점과 $C$점을 대입해도 성립한다는 것이다.
따라서 직접 대입해보자.
먼저 $A$점을 대입하면, $m+n+3=0$이 되어 식을 정리하면 $m+n=-3$이 된다.
그다음 $C$점을 대입하면 $s+t+3=0$이 되어 식정리를 하면 $s+t=-3$이 된다.
자 이제 $-3x+y-1=0$이라는 직선은 $B \left(p, q\right)$와 $C\left(s, t\right)$를 지난다.
마찬가지로 그 두 점을 직선의 방정식에 대입해 보자.
먼저 $C$점을 대입하면 $-3p+q-1=0$이 되어 식정리를 하면 $-3p+q=1$이 된다,.
그다음 $C$점을 대입하면 $-3s+t-1=0$이 되어 식정리를 하면 $-3s+t=1$이 된다.
이렇게 두 직선에 점 4개를 대입하며 얻은 식이 총 4개가 있다.
그 식을 다시 한번 써보면 아래와 같다.
$$m+n=-3$$
$$s+t=-3$$
$$-3p+q=1$$
$$-3s+t=1$$
자 이제 문제에서는 $m+q+n-s-3p-t$을 구하라고 되어 있다.
$m+q+n-s-3p-t$을 예쁘게 괄호를 이용하여 여러분이 보기 쉽게 정리해 보겠다.
$$m+q+n-s-3p-t$$
$$=\left(m+n\right)+\left(-3p+q\right)-\left(s+t\right)$$
$$=\left(-3\right)+\left(1\right)-\left(-3\right)$$
$$=-3+1+3=1$$
따라서 정답은 $1$이 되는 것이다.
'중고등 수학' 카테고리의 다른 글
| 중1 수학. 점, 선, 면 (18) | 2023.07.08 |
|---|---|
| 중2 수학 1학기 기말고사 일차함수 활용 기출문제 풀이 (19) | 2023.07.08 |
| 중1 수학. 최소공배수 용어 정리 (43) | 2023.07.06 |
| 중1 수학. 최대공약수 용어 정리 (10) | 2023.07.06 |
| 중2 수학. 미지수가 2개인 일차방정식 문제풀이 (48) | 2023.07.05 |