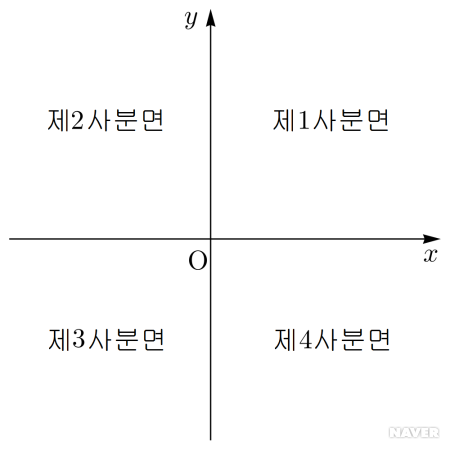
사분면
사분면은 좌표평면을 위의 그림처럼 4곳으로 나누어 이름을 붙인 것이다.
사분면의 이름은 제1사분면을 기준으로 시계 반대 방향으로 되어 있다.
좌표평면 위의 점 $\left(x,y \right)$가
제1 사분면 위의 점이면 $x>0, y>0$
제2 사분면 위의 점이면 $x<0, y>0$
제3 사분면 위의 점이면 $x<0,y<0$
제4 사분면 위의 점이면 $x>0,y<0$이다.
부호에 대해 좀 어렵게 느껴진다면 한국말로 편하게 설명하자면 아래와 같다.
제1 사분면 위의 점이면 오른쪽 위 이므로 $x, y$부호가 양수 양수이다.
제2 사분면 위의 점이면 왼쪽 위 이므로 $x, y$부호가 음수 양수이다.
제3 사분면 위의 점이면 왼쪽 아래이므로 $x, y$부호가 음수 음수이다.
제4 사분면 위의 점이면 오른쪽 아래이므로 $x, y$부호가 양수 음수이다.
이러한 방식으로 머릿속에 사분면을 그려서 위치로 파악하는 것이 편할 수도 있다.
참고로 좌표축 위의 점은 어느 사분면에도 속하지 않는다.
실제 점이 몇 사분면인지 알아보자.
$A\left(-1,5\right)$는 왼쪽 위에 위치하므로 제2 사분면의 점이다.
$B\left(0,-2\right)$는 $y$축의 아래로 2칸 내려가 있다. 즉 $y$축 위의 점이므로 어느 사분면도 아니다.
$C\left(5,-9\right)$는 오른쪽 아래에 있는 점이므로 제4 사분면의 점이다.
만약 $a>0. b<0$일 때
$A\left(a,b\right)$는 양수, 음수이고 이 말은 오른쪽 아래에 위치하여, 제4 사분면 위의 점이다.
$B\left(a,-b\right)$에서 $a$는 양수이고, $-b$는 양수이므로 오른쪽 위에 위치하며 제1 사분면 위의 점이다.
$C\left(-a,-b\right)$에서 $-a$는 음수이고, $-b$는 양수이므로 왼쪽 위에 위치하여 제2 사분면 위의 점이다.
'중고등 수학' 카테고리의 다른 글
| 중1 수학. 반비례 관계의 활용 (24) | 2023.06.30 |
|---|---|
| 중1 수학. 정비례 관계의 활용 (55) | 2023.06.29 |
| 중1 수학. 일차방정식의 활용-소금물, 농도 (59) | 2023.06.28 |
| 중1 수학. 일차방정식의 활용-거리, 속력, 시간 (52) | 2023.06.27 |
| 중1 수학. 일차방정식 활용- 나이 (78) | 2023.06.25 |