반응형
사분면을 이용한 문제 풀이
문제.
점$A\left(-a,~b\right)$가 제$2$사분면 위의 점일 때, 점$B\left(a,~-b\right)$는 제 몇 사분면 위의 점인가?
필요한 개념
사분면: 좌표평면의 구역을 4곳으로 나누었을때 오른쪽 위는 제1사분면이다.
왼쪽 위는 제2사분면이다.
왼쪽 아래는 제3사분면이다.
오른쪽 아래는 제4사분면이다.
이때 각 사분면의 부호를 나타내보면 아래와 같다.
제1사분면의 부호는 $\left(+,~+\right)$이다.
제2사분면의 부호는 $\left(-,~+\right)$이다.
제3사분면의 부호는 $\left(-,~-\right)$이다.
제4사분면의 부호는 $\left(+,~-\right)$이다.
풀이.
일단 문제를 다시한번 파악해 보자.
점$A\left(-a,~b\right)$가 제$2$사분면 위의 점일 때, 점$B\left(a,~-b\right)$는 제 몇 사분면 위의 점인가?
$A\left(-a,~b\right)$가 제$2$사분면 위의 점이므로 $-a<0,~b>0$이다.
따라서 $a>0,~b>0$이다.
또한 문제에서 점$B\left(a,~-b\right)$가 몇 사분면인지 구하라고 하였으므로 $a,~-b$의 부호를 알아야 한다.
$a>0,~b>0$에서 $a>0$이고 $-b<0$이므로 오른쪽 아랫부분을 의미한다.
따라서 $B\left(a,~-b\right)$는 제4사분면이다.
728x90
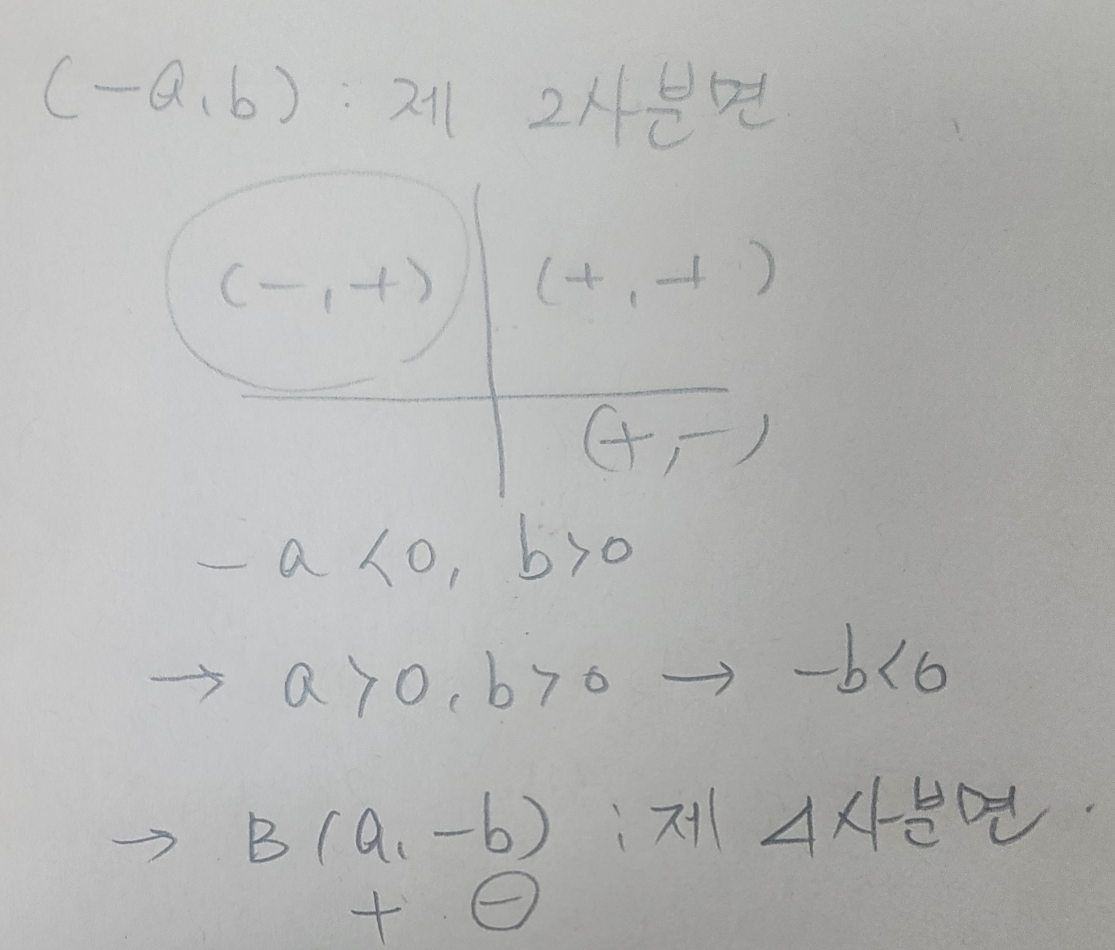
반응형
'중고등 수학' 카테고리의 다른 글
| 중3 수학. 근의공식을 이용한 문제 풀이 (40) | 2023.10.21 |
|---|---|
| 중3 수학. 이차방정식의 활용-잘못 세운 식 (32) | 2023.10.19 |
| 고등 수학. 나머지 정리 문제 풀이. (4) | 2023.10.16 |
| 중1 수학. 일차식의 계산. 괄호 풀기 (4) | 2023.10.15 |
| 중3 수학. 제곱근의 소수 부분을 이용한 문제 풀이 (2) | 2023.10.14 |