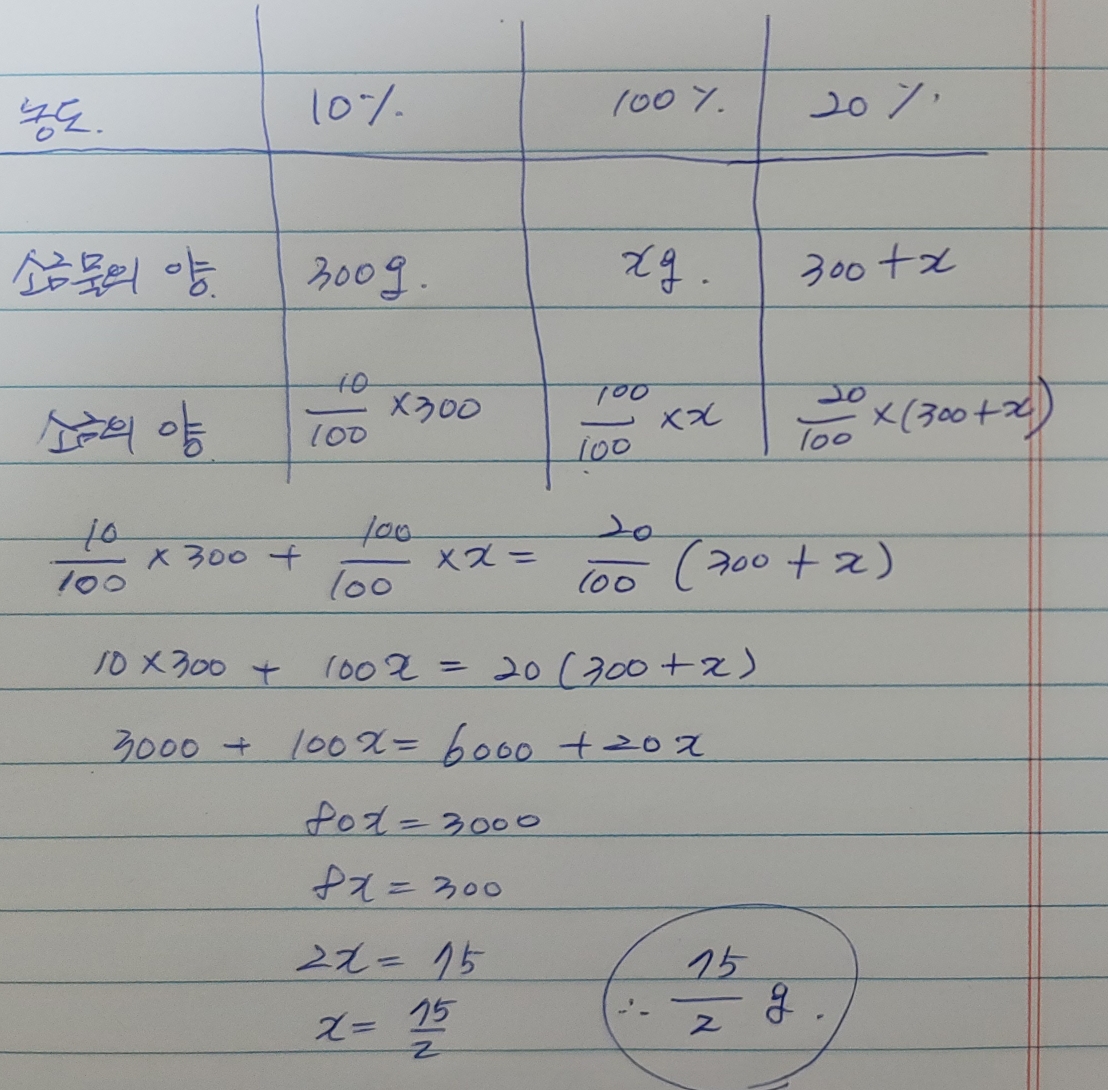교육

중1 수학. 일차방정식 활용 소금물 문제 풀이문제.$10\%$의 소금물 $300g$이 있다. 여기에 몇 $g$의 소금을 더 넣으면 $20\%$의 소금물이 되는지 구하시오. 필요개념$소금의 양=\frac{농도}{100}\times 소금물의 양$ 풀이.자세한 풀이과정은 아래 사진을 참고하셔도 됩니다. 소금물 문제는 표를 이용하여 문제를 해결하는 것이 좋다. 그리고 소금의 양을 이용하여 식을 세우면 된다. 먼저 농도 $10\$$소금물에 대한 소금의 양은 $\frac{10}{100}\times 300$이다. 더불어 소금을 더 넣었기 때문에 소금의 농도는 $100\%$이고 더 넣은 소금의 양$x~g$이라 하자. 그 두 개를 섞어서 농도가 $20\%$소금물이 되었을 때, $20\%$에 대한 소금의 양은 $\frac..

일차방정식의 활용, 시계문제 일차방정식에서 시침과 분침이 움직인 각도를 이용한 활용문제를 다루어보고자 한다. 시침과 분침이 움직이는 각도는 12시 0분을 기준으로 움직이는 각도를 이야기할 것이다. 먼저 시침이 움직이는 각도를 알아보자. 시침은 12시간을 기준으로 $360^{o}$ 움직인다. 이것을 12로 나누면 시침은 1시간 기준으로 $30^{o}$ 움직인다. 1시간은 60분이 되므로 시침은 60분동안 $30^{o}$움직인다. 이것을 다시 60으로 나누면 시침은 1분동안 $\frac{1}{2}=0.5^{o}$움직인다. 다시 한번 정리하겠다. 시침은 $$12시간에 360^{o}움직인다.$$ $$1시간에 30^{o}움직인다.$$ $$1분에 0.5^{o}움직인다$$ 자 이제 분침을 이야기해보자. 분침은 60분..

일차방정식의 활용- 소금물 농도 먼저 농도에 관한 일차방정식의 활용 문제를 풀기 전 알아야 할 중요한 공식이 있다. $$소금의 양=\frac{농도}{100}\times 소금물의 양$$ 반드시 알아야 할 공식이다. $3$%소금물 $100g$과 $15$% 소금물을 섞어서 $7$% 소금물을 만들었다. 이때 섞은 $15$% 소금물은 몇 $g$인가? 이런 유형의 문제를 풀기 위해서는 표름 만들어서 푸는 것이 가장 확실한 방법이다. 표의 기본틀은 아래의 표를 채워나가면 되는 것이다. 농도 소금물의 양 소금의 양 위의 표를 문제를 읽고 순서대로 채워나가 보자. 농도 3% 15% 7% 소금물의 양 소금의 양 일단 농도만 채워보았다. 그리고 3%의 소금물은 $100$g이므로 아래 $100$을 써넣는다. $15$% 소금물..

일차방정식의 활용- 거리, 속력, 시간자 먼저 거리 속력 시간에 대한 공식을 초등학교 때 배웠다. $$거리=속력\times 시간$$ $$속력=\frac{거리}{시간}$$ $$시간=\frac{거리}{속력}$$ 이 세 가지 공식은 반드시 암기해야 하는 상황이다. 특히 $거리=속력\times 시간$은 암기할 때 '거리에 나가면 속이 시원하다'로 암기하면 얼굴은 붉어지겠지만, 머리는 화끈하게 암기가 될 것이다.행복이는 등산을 하는데 올라갈 때는 시속 $2km$로 걷고, 내려올 때는 같은 등산로를 시속 $5km$로 걸었더니 총 $5$시간이 걸렸다. 등산로의 길이를 구하여라.등산로의 길이를 $xkm$라 하자. 올라갈 때 시간 + 내려올 때 시간 = 5시간인 것을 이용하여 식을 세워보자. $$올라갈 때 시간 = \f..

일차방정식 활용 나이문제 활용문제의 개념은 문제를 잘 읽고 식을 세워서 풀어낸 후 문제에 맞는 답을 찾고 검토하여 맞는지 확인해야 한다. 이것이 개념이다, 개념을 완벽히 안다고 해서 모든 문제를 풀어낼 수는 없다. 따라서 문제를 보고 몇 번 연습을 해야 한다. 자 이제 실제 문제를 보고 연습해보자. 형과 동생의 나이차는 $4$살이고, 나이의 합은 $48$살일 때 동생의 나이를 구하여라. 동생의 나이를 $x$살이라 하자. 형의 나이는 동생보다 당연히 나이가 많고 $4$살 차이이므로 형의 나이는 $x+4$살이 된다. 문제에서 동생과 형의 나이 합이 $48$살이므로 식을 세워보자. $$x+\left(x+4\right)=48$$ $$2x+4=48$$ $$2x=48-4$$ $$2x=44$$ $$x=22$$ 따라서..

일차방정식 활용 돈문제 $200$원짜리 사탕과 $300$원짜리 과자를 합하여 $17$개를 사고 $4400$원의 돈을 지불하였다. 이때, 과자는 몇 개 샀는가? 과자의 갯수를 $x$개라 하자. 과자와 사탕을 합쳐서 $17$개를 샀으므로, 사탕의 개수는 $\left(17-x\right)$개로 둘 수 있다. 과자를 산 금액은 $300x$원 사탕을 산 금액은 $200\left(17-x\right)$원이다. 총 지불 금액은 $4400$원이므로 이제 식을 세우고 풀어보자. $$200\left(17-x\right)+300x=4400$$ 여기서 양 변을 $100$으로 나누면 $$2\left(17-x\right)+3x=44$$ $$34-2x+3x=44$$ $$-2x+3x=44-34$$ $$x=10$$ 따라서 과자를 총 ..

일차방정식의 활용 - 숫자실제 여러 가지 문제를 살펴보며 식을 세우고 풀어보자.어떤 수에 $10$을 더한 수는 어떤 수의 $4$배보다 $1$만큼 클 때, 어떤 수는 무엇일까?어떤 수를 $x$라 하자. 어떤 수에 $10$을 더한 수 : $ x+10$ 어떤 수의 $4$배보다 $1$만큼 크다. : $4x+1$ 즉 일차방정식을 세우면 $$x+10=4x+1$$ $$x-4x=1-10$$ $$-3x=-9$$ $$x=3$$ 따라서 어떤 수는 $3$이 된다.어떤 수의 $2$배에 $10$을 더한 수는 어떤 수의 $3$배와 같다. 어떤 수는 무엇일까?어떤 수를 $x$라 하자. 어떤 수의 $2$배에 $10$을 더한 수 : $2x+10$ 어떤 수의 $3$배 : $3x$ 즉 일차방정식을 세워보면 $$2x+10=3x$$ $$2x-..