젠센 형태 함수방정식
젠센 형태 함수방정식(Jensen's functional equation)은 수학의 여러 분야에서 중요한 역할을 하는 함수 방정식입니다. 이 방정식은 주로 확률론, 통계학, 그리고 함수 해석학에서 사용됩니다. 젠센의 불평등(Jensen's inequality)과 밀접한 관련이 있으며, 주어진 함수가 볼록 함수일 때, 이 방정식은 특정한 성질을 갖는 함수의 형태를 규명하는 데 사용됩니다.
1. 젠센 형태 함수방정식의 정의
젠센 형태 함수방정식은 다음과 같은 형태로 표현됩니다:
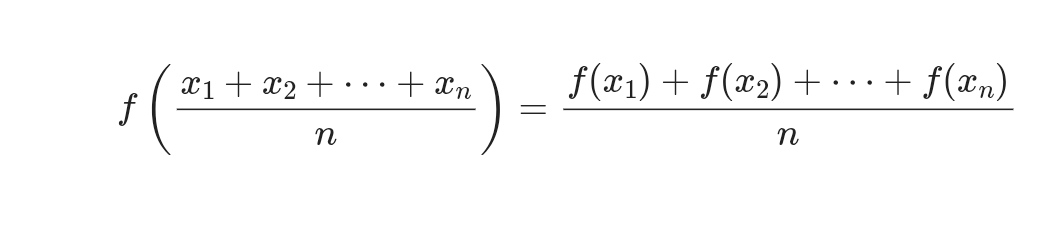
여기서 $f$는 정의역이 실수인 함수이며, $x_1, x_2, \ldots, x_n$은 실수입니다. 이 방정식은 $f$가 볼록 함수일 때 성립합니다. 즉, 함수 $f$가 볼록 함수일 경우, 입력값의 평균에 대한 함수의 값은 입력값 각각에 대한 함수의 값의 평균과 같습니다.
2. 볼록 함수와 젠센의 불평등
볼록 함수의 정의는 다음과 같습니다. 함수 $f$가 정의역 $I$에서 볼록하다는 것은 임의의 두 점 $x_1, x_2 \in I$와 $t \in [0, 1]$에 대해 다음이 성립하는 경우입니다:
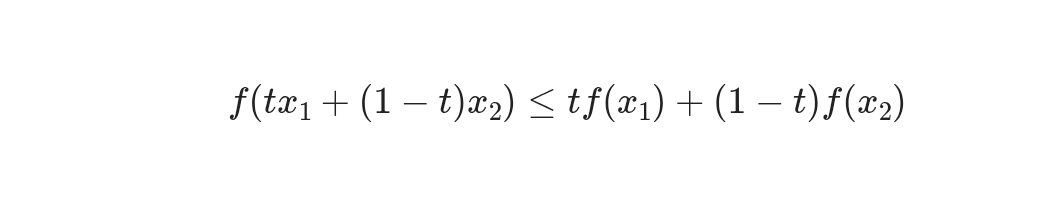
이 정의는 함수의 그래프가 두 점을 연결하는 직선 아래에 위치함을 의미합니다. 젠센의 불평등은 이러한 볼록 함수의 성질을 이용하여, 확률 변수의 기대값에 대한 불평등을 제공합니다. 즉, 확률 변수 $X$가 있을 때, $f$가 볼록 함수라면 다음이 성립합니다:
$$
f(E[X]) \leq E[f(X)]
$$
3. 젠센 형태 함수방정식의 해
젠센 형태 함수방정식의 해는 주로 선형 함수와 관련이 있습니다. 즉, $f(x) = ax + b$ 형태의 함수가 이 방정식을 만족합니다. 여기서 $a$와 $b$는 상수입니다. 이 외에도, 특정한 조건을 만족하는 비선형 함수도 해가 될 수 있습니다.
3.1. 선형 함수의 경우
선형 함수는 젠센 형태 함수방정식을 만족하는 가장 간단한 형태입니다. 예를 들어, $f(x) = ax + b$를 대입하면 다음과 같은 결과를 얻습니다:
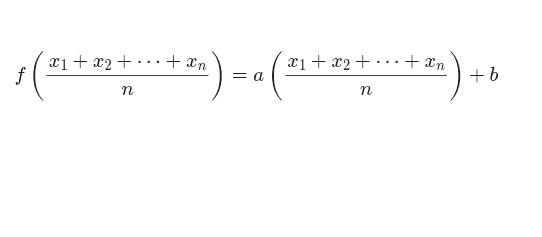
그리고 오른쪽 항은 다음과 같습니다:
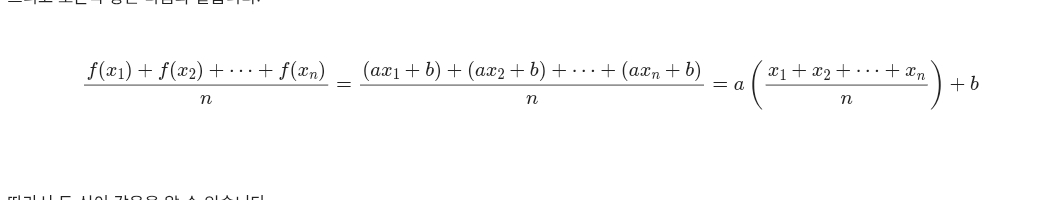
따라서 두 식이 같음을 알 수 있습니다.
3.2. 비선형 함수의 경우
비선형 함수의 경우, 젠센 형태 함수방정식의 해는 더 복잡할 수 있습니다. 예를 들어, 특정한 비선형 함수가 볼록성을 만족할 경우, 젠센 형태 함수방정식을 만족할 수 있습니다. 이러한 함수들은 일반적으로 특정한 조건을 만족해야 하며, 그 조건은 함수의 형태에 따라 다릅니다.
4. 응용 분야
젠센 형태 함수방정식은 여러 분야에서 응용됩니다. 특히, 통계학에서는 데이터의 평균과 분산을 다룰 때, 확률론에서는 확률 변수의 기대값을 계산할 때 자주 사용됩니다. 또한, 경제학에서는 효용 함수의 분석에 활용되며, 최적화 문제에서도 중요한 역할을 합니다.
젠센 형태 함수방정식은 수학적 분석에서 중요한 도구로, 볼록 함수의 성질을 이해하고 활용하는 데 필수적입니다. 이 방정식은 다양한 분야에서 응용되며, 함수의 형태를 규명하는 데 도움을 줍니다. 젠센의 불평등과 함께, 이 방정식은 확률론과 통계학의 기초를 형성하는 중요한 개념입니다.
'자연과학, IT, 공학' 카테고리의 다른 글
| 상태공간방정식 (2) | 2025.02.02 |
|---|---|
| 수정 완경사 방정식 (3) | 2025.02.01 |
| 로드카볼테라방정식 (2) | 2025.01.29 |
| 프롤로테라피 (16) | 2025.01.20 |
| PDLC 필름에서 1차상전이와 2차상전이 (5) | 2025.01.16 |