로드카볼테라방정식
로드카볼테라 방정식(Roads-Cavalieri Equation)은 수학과 물리학에서 중요한 역할을 하는 방정식으로, 주로 비선형 동역학 시스템의 해석에 사용됩니다. 이 방정식은 특정한 형태의 비선형 미분 방정식을 다루며, 주로 생물학적, 경제적, 물리적 시스템의 모델링에 활용됩니다.
1. 로드카볼테라 방정식의 정의
로드카볼테라 방정식은 일반적으로 다음과 같은 형태로 표현됩니다:
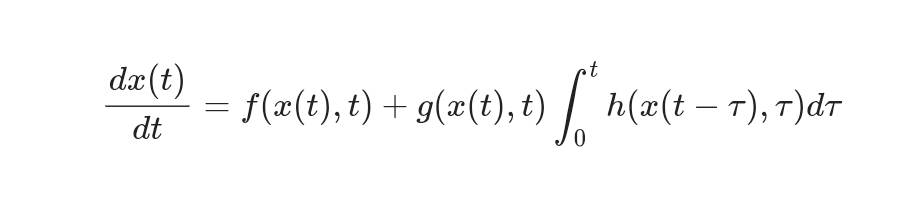
여기서:
- $x(t)$는 시간 $t$에 따른 상태 변수입니다.
- $f(x(t), t)$는 시스템의 현재 상태와 시간에 의존하는 함수입니다.
- $g(x(t), t)$는 시스템의 현재 상태에 따라 달라지는 계수입니다.
- $h(x(t - \tau), \tau)$는 과거 상태에 의존하는 함수로, 시스템의 메모리 효과를 나타냅니다.
이 방정식은 시스템의 현재 상태가 과거의 상태에 의존하는 경우를 모델링하는 데 유용합니다.
2. 역사적 배경
로드카볼테라 방정식은 20세기 중반에 로드(Road)와 카볼테라(Cavalieri)라는 두 수학자에 의해 발전되었습니다. 이들은 비선형 시스템의 동역학을 연구하면서 이러한 형태의 방정식을 도출하였고, 이후 다양한 분야에서 응용되었습니다.
3. 응용 분야
로드카볼테라 방정식은 여러 분야에서 활용됩니다:
- 생물학: 생태계 모델링, 인구 성장, 전염병 확산 등의 문제를 다룰 때 사용됩니다. 예를 들어, 특정 종의 개체 수가 과거의 개체 수에 따라 어떻게 변화하는지를 설명할 수 있습니다.
- 경제학: 경제 시스템의 동적 모델링에 사용되며, 소비자 행동, 시장의 변화 등을 분석하는 데 유용합니다.
- 물리학: 물리적 시스템의 동역학을 설명하는 데 사용되며, 특히 비선형 현상이나 복잡한 상호작용을 다룰 때 효과적입니다.
4. 해석 및 해법
로드카볼테라 방정식의 해를 구하는 것은 일반적으로 쉽지 않습니다. 비선형성과 적분 항의 존재로 인해 해를 구하기 위한 다양한 수치적 방법이 필요합니다. 대표적인 방법으로는 다음과 같은 것들이 있습니다:
- 수치적 적분: 과거 상태에 대한 적분을 수치적으로 계산하여 해를 근사합니다.
- 선형화: 비선형 항을 선형화하여 근사적인 해를 구하는 방법입니다.
- 시뮬레이션: 컴퓨터를 이용한 시뮬레이션을 통해 시스템의 동적 행동을 분석합니다.
5. 예제
간단한 예로, 로드카볼테라 방정식을 사용하여 인구 성장 모델을 살펴보겠습니다. 인구 $N(t)$가 시간에 따라 변화하는 경우, 다음과 같은 방정식을 설정할 수 있습니다:
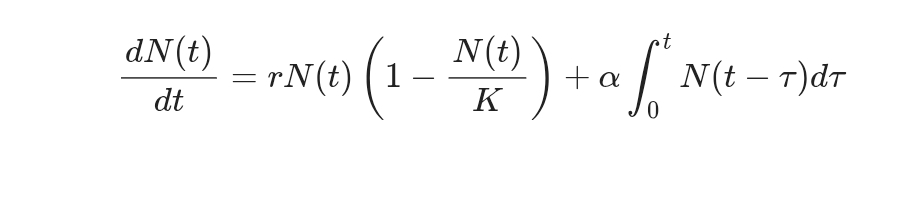
여기서:
- $r$은 성장률,
- $K$는 환경의 수용력,
- $\alpha$는 과거 인구의 영향을 나타내는 계수입니다.
이 방정식은 현재 인구가 과거 인구에 의존하는 복잡한 동적 시스템을 모델링합니다.
로드카볼테라 방정식은 비선형 동역학 시스템을 이해하고 분석하는 데 중요한 도구입니다. 다양한 분야에서의 응용 가능성과 복잡한 시스템의 동적 행동을 설명하는 데 유용한 이 방정식은 앞으로도 많은 연구와 발전이 기대됩니다. 이러한 방정식을 통해 우리는 복잡한 현상을 보다 잘 이해하고 예측할 수 있는 기회를 가지게 됩니다.
'자연과학, IT, 공학' 카테고리의 다른 글
| 수정 완경사 방정식 (3) | 2025.02.01 |
|---|---|
| 젠센 형태 함수방정식 (7) | 2025.01.31 |
| 프롤로테라피 (16) | 2025.01.20 |
| PDLC 필름에서 1차상전이와 2차상전이 (5) | 2025.01.16 |
| 자산유동화 및 부동산 투자신탁(REITs) (11) | 2024.12.27 |